10203. Arctic network
The Department of
National Defense (DND) wishes to connect several northern outposts by a
wireless network. Two different communication technologies are to be used in
establishing the network: every outpost will have a radio transceiver and some
outposts will in addition have a satellite channel.
Any two outposts
with a satellite channel can communicate via the satellite, regardless of their
location. Otherwise, two outposts can communicate by radio only if the distance
between them does not exceed d, which
depends of the power of the transceivers. Higher power yields higher d but costs more. Due to purchasing and
maintenance considerations, the transceivers at the outposts must be identical;
that is, the value of d is the same
for every pair of outposts.
Your job is to
determine the minimum d required for
the transceivers. There must be at least one communication path (direct or
indirect) between every pair of outposts.
Input. The first line contains the number n of test cases. The first line of each
test case contains the number of satellite channels s (1 ≤ s ≤ 100)
and the number of outposts p (s < p ≤ 500). p lines follow, giving the (x, y)
coordinates of each outpost in km (coordinates are integers
between 0 and 10000).
Output. For each
case print the minimum d required to
connect the network. Output should be specified to 2 decimal points.
|
Sample
input |
Sample
output |
|
1 2 4 1 0 3 0 6 0 7 2 |
2.24 |
SOLUTION
graphs – Prim algorithm
Algorithm analysis
Start Prim’s algorithm.
Construct an array dist, where dist[i] stores the length of the shortest
edge from MST that runs to the vertex i.
That is, MST consists of these edges. Moreover, dist[0] = 0, since we start the
algorithm from the vertex 0.
At the end of Prim’s algorithm,
sort the dist array. The most distant
outposts should be connected by satellite channels. They should be placed in
those s outposts that connect the
longest edges from dist (s – 1 edges connect s outposts). Therefore, the desired value of d will be the length of the edge that is the s-th from the end of dist.
Example
Consider the graph given
in a sample.
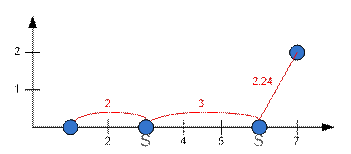
Put two satellite
channels at points (3; 0) and (6; 0). Thus, the outposts in these coordinates
are connected via satellite. Find
the largest one among the remaining edges of MST. This will be the edge
connecting the points (6; 0) and (7; 2), its length is 2.24.
Algorithm realization
Declare
global arrays. Store the coordinates of the outposts in (x[i], y[i]).
used[i] = 1, if vertex i is included in MST.
#define MAX 501
#define INF
0x3F3F3F3F
int x[MAX], y[MAX];
int used[MAX],
dist[MAX];
The function dist2 computes the squared distance
between outposts i and j.
int dist2(int i, int j)
{
return (x[j] -
x[i])*(x[j] - x[i]) +
(y[j] - y[i])*(y[j] -
y[i]);
}
Function Prim implements the Prim’s
algorithm.
void Prim(void)
{
Initialize the arrays.
memset(dist,
0x3F, sizeof(dist));
memset(used,
0, sizeof(used));
Start building the MST from the vertex 0. Initialize dist[0] = 0, used[0] = 1.
int i,
j, cur = 0;
dist[cur]
= 0;
used[cur]
= 1;
Make n – 1 iterations. At each iteration, add
one vertex to MST (so n – 1 vertices should be
added to MST).
for (i =
1; i < n; i++)
{
The current vertex is cur. Iterate over the edges (cur, j)
and recalculate the value of dist[j].
Thus dist[j] stores the current
shortest distance from vertex
j to the current MST.
for (j =
0; j < n; j++)
if
(!used[j] && (dist2(cur, j) < dist[j]))
dist[j] = dist2(cur, j);
We are looking for the shortest edge that will be included in MST. To do this, look for the smallest dist[j] such that the vertex j does not yet belong
to MST (used[j] = 0). The number of the vertex with
the smallest dist[j] is stored into cur (it becomes the current one).
int min
= INF;
for (j =
0; j < n; j++)
if
(!used[j] && (dist[j] < min))
{
min = dist[j];
cur = j;
}
Vertex cur is included to MST.
used[cur]
= 1;
}
}
The main part of the program. Process tests tests.
scanf("%d", &tests);
while (tests--)
{
Read
the input data.
scanf("%d
%d", &s, &n);
for (i =
0; i < n; i++)
scanf("%d
%d", &x[i], &y[i]);
Run
the Prim’s algorithm.
Prim();
Sort
the array dist.
sort(dist,
dist + n);
Print
the answer.
printf("%.2lf\n",
sqrt(dist[n - s]));
}
Java realization
import java.util.*;
public class Main
{
static int n;
static int x[], y[];
static int used[], dist[];
static int
dist2(int i, int j)
{
return (x[j] - x[i])*(x[j] - x[i]) +
(y[j] - y[i])*(y[j] - y[i]);
}
static void
Prim()
{
dist = new int[n];
Arrays.fill(dist,
Integer.MAX_VALUE);
used = new int[n];
int i, j, cur = 0;
dist[cur] =
0;
used[cur] =
1;
for (i = 1;
i < n; i++)
{
for (j = 0;
j < n; j++)
if (used[j] ==
0 && dist2(cur, j)
< dist[j])
dist[j] = dist2(cur, j);
int min =
Integer.MAX_VALUE;
for (j = 0;
j < n; j++)
if (used[j] ==
0 && dist[j]
< min)
{
min = dist[j];
cur = j;
}
used[cur] =
1;
}
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int tests = con.nextInt();
while (tests--
> 0)
{
int s = con.nextInt();
n = con.nextInt();
x = new int[n];
y = new int[n];
for (int i = 0;
i < n; i++)
{
x[i] = con.nextInt();
y[i] = con.nextInt();
}
Prim();
Arrays.sort(dist);
System.out.println(Math.sqrt(dist[n - s]));
}
con.close();
}
}